The Tarot of Ideals

More Spreads

Reading without a “spread”

Sometimes it helps to just lay cards down and look at them, with or without asking a question; it can serve as a kind of card meditation.  One ponders the relationships, sometimes linear, other times more complex.  The supporting and opposing suits are usually taken into consideration.  The court cards may be seen as directing or leading the numbered cards, and trump cards generally take center stage.

For example, here are three cards, chosen without any particular forethought:

Eight of swords | Five of coins | Knight of swords

The two swords are “ganging up” on the five of coins; their suits oppose each other, and the five itself suggests instability or change.  The knight represents vigor, and the eight power, so this is quite a situation for the center card; something big may be about to happen.

Here, I was thinking about impending changes that were about to take place at work:

Two of coins | King of coins | Death | Queen of rods | The Tower

I usually associate coins with the workplace.  Reading the cards in sequence, a duality, in context probably a conflict, is assoicated with a “boss” role and Death, hopefully figurative; a position was in fact about to end.  But on the other side of death is a rescuer of sorts, either a literal nurturing figure, or the preservation of a truly supporting role, leading to some sort of revolution.

Here, a cups card is on one end, opposed by swords and rods.  But the ace may be able to hold its own; it is a strong card in general, independent and self-sufficient:

Ace of cups | Ten of swords | Four of rods | Page of rods | Three of swords

Finally, we see a trump card, in this case the grand figure of the Papesse, literally taking center stage.  But she is surrounded by three coins.  One tends not associate her with earthly affairs; this may indicate that she is being tempered by, or perhaps rising above, the simple and pragmatic:

Nine of coins | Three of coins | The Papesse | Two of cups | Queen of coins

One need not lay down the cards in a linear sequence; let your imagination be your guide.  The following are a few novel alternatives.

Three-dimensional spreads:  the Tetrahedron

Lately, this one has been my favorite spread.  A tetrahedron may be thought of as a triangular pyramid, with an apex and three points forming a base.  But it may also be thought of as two lines at right angles, like axes, but not in the same plane.  In either case, it is fully symmetrical; it may be rotated so that any point is the apex, or any two line segments form the axes.  (To visualize this, it helps to examine a physical model; I have one in front of me made of toothpicks and chewable vitamins.)

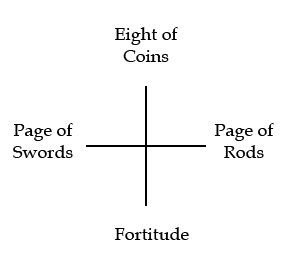
Any four cards may be considered a tetrahedron.  And because of the symmetry, the actual positions of the cards are of no consequence.  Look for either opponent pairs, or an apex.  In the following case, the Pages, rods and swords, make a natural pair, contrasted against the eight of coins and Fortitude:

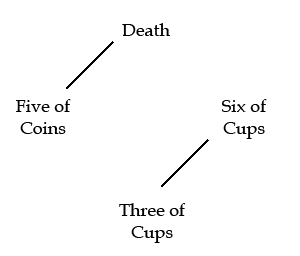
Here, the cups form a natural pair.  Remember, any two cards may represent an axis; the shape may be freely rotated:

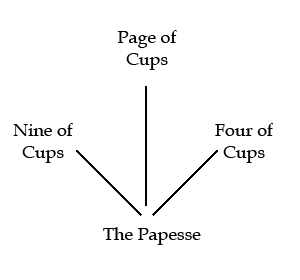
Here, the Papesse is the apex, and an appropriate element is the base:

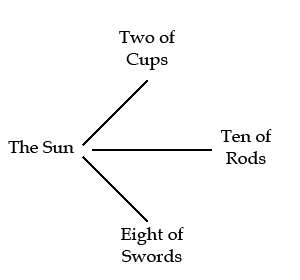
I was thinking about an action that I had taken this week; it is nice to see the sun shining on such a diverse world:

Three-dimensional spreads:  the octahedron

An octahedron is a little more complex.  The shape is basically two square-based pyramids fused together, base to base.  The apices of each pyramid form an axis that runs through a central square.  But note the threefold symmetry; there are three pairs of apices that pierce three squares, depending on how you look at it:

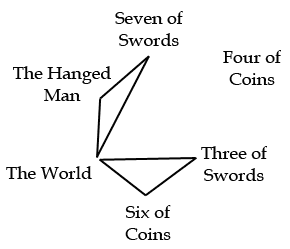
When laying down six cards to form an octahedron, the positions of the opposing cards are what is significant.  One looks for an opposing pair that forms an axis running through a square made by the other four cards.  In the following case, one way to look at it is that the mundane, physical world, represented by the four of coins, is being transformed into the World card:

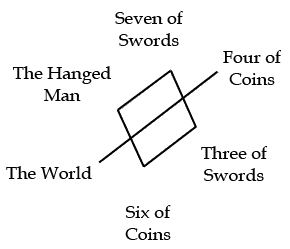
The two swords form one side of the central square, and oppose the Hanged Man and the six of coins.  Note that the square may rotate around the axis; the orientation of the cards on the square relative to the four of coins and the World is arbitrary.

A more complicated method is to look at the groups of three cards that form the triangular faces of the octahedron.  Here they are drawn radiating out from the cards on the axis above:

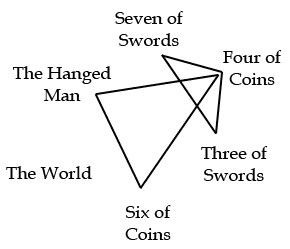
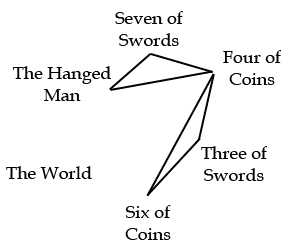
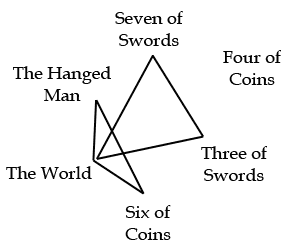
If you would like to play with these and some other shapes, check out mathsisfun.com:

mathsisfun.com/geometry/tetrahedron.html
mathsisfun.com/geometry/octahedron.html