
Dynamic Line Energies
marbles | playing cards | how-to
The traditional yarrow stalk method and the 3-coin method yield different odds for determining hexagram lines. The former’s are 1:5:7:3 for moving yin, yang, yin, and moving yang, respectively, resulting in a higher probability for moving yang (3:5) than moving yin (1:7). The 3-coin method’s are 1:3:3:1, with equal probability of moving yin and yang (1:3). This discrepancy is a source of some controversy among I Ching users. Besides the question of which is “better,” the significance of the odds themselves raises questions, as the results are intended to be synchronistic, or oracular, rather than simply random.
One could bypass the question to an extent by making the odds a part of the selection process. Imagine if each line type’s odds of moving vs. not were not fixed, but allowed to change as part of the process. This would allow the process to determine its own odds, each new hexagram having its own “yin energy” and “yang energy,” and would add a chaotic, less predictable element to the result. Spoiler alert: my preferred method is to use playing cards; you can jump straight to that section if you want.
My original idea was to start with three groups of beads or marbles, distributed as follows: 4 yin and 4 yang in the first group, 4 yin and 4 moving yin in the second, and 4 yang and 4 moving yang in the third. Four beads are selected at random from each of the second and third groups, and added to the first to make a total of 16 with odds for moving lines chosen at random. One then selects each hexagram line as in “the way of sixteen”: mix up the beads in the first container and choose one at random; the color determines the line type. Then return the bead to the container and repeat five times to complete the hexagram.


This method preserves the odds of getting a yin vs. yang line in general. There are always 8 lines of each type; only the odds of getting a moving line vary. The method itself is somewhat cumbersome, requiring sorting the beads into three groups each time; is there an easier way? Yes, one could start with all 24 beads together, and simply remove a number of beads at the start so that the odds of getting any line type are no longer known.
Using beads or marbles
Imagine starting with 24 marbles, distributed in the conventional coin ratio of 3:9:9:3. The probability of getting either moving line is always 1/8, or 0.125. If one removes 6 marbles, leaving 18 to choose hexagram lines from, the distribution of probabilities of getting either moving line is now as follows:
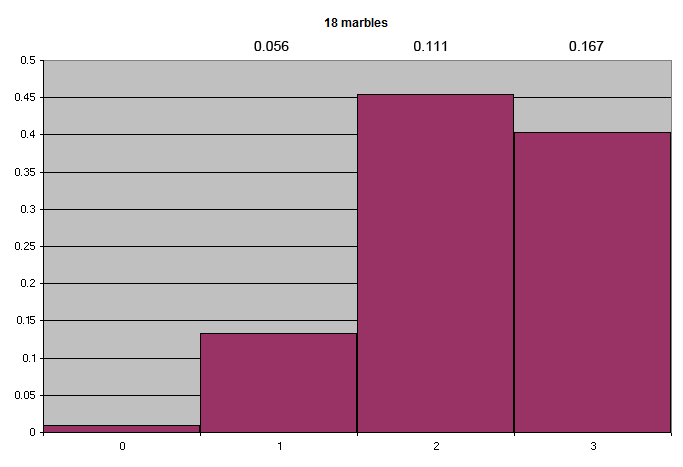
The graph illustrates that the odds of getting 2 moving line marbles of either type in the resulting 18 are 0.454, or 45.4%; and when consulting the I Ching with that number of marbles, the odds of getting a moving line are 2/18, or 0.111.
What about the overall ratio of yin and yang lines? This too is subject to variation, as follows:
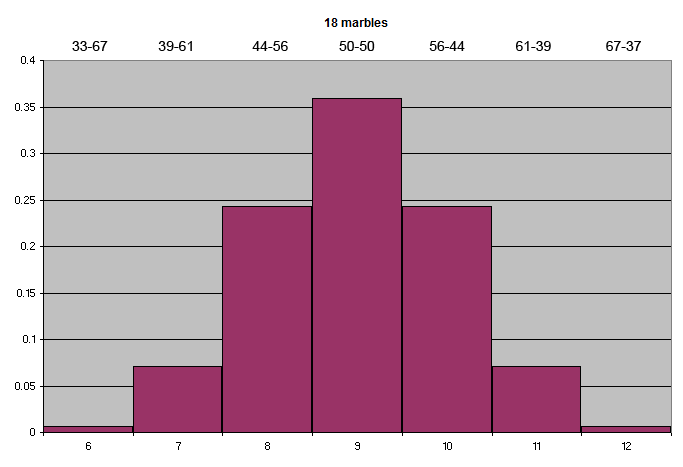
The odds of the 18 marbles consisting of 8 yang and 10 yin are 0.243, or 24.3%; the ratio of yin to yang lines in that case is about 44-56.
This introduces a new element into the selection of I Ching lines: the process determines its own probabilities. Neither the stable nor moving lines are locked into a fixed ratio, as they are with either coins or yarrow stalks, and one need not choose between them. The choice that determines the odds is how many marbles are removed from the original number.
If one removes 8 marbles, leaving 16, the odds are skewed even more. Here are the moving line probabilities; note that the odds of getting zero moving lines of either type in the final 16 are close to 3%, as opposed to 1% for 18 marbles:
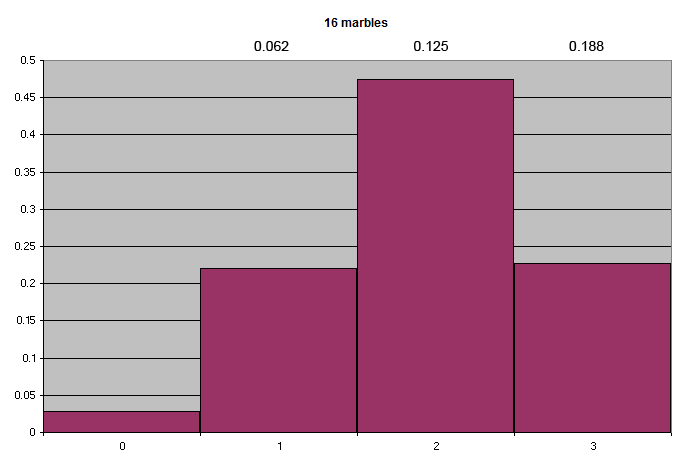
The overall line probabilities:
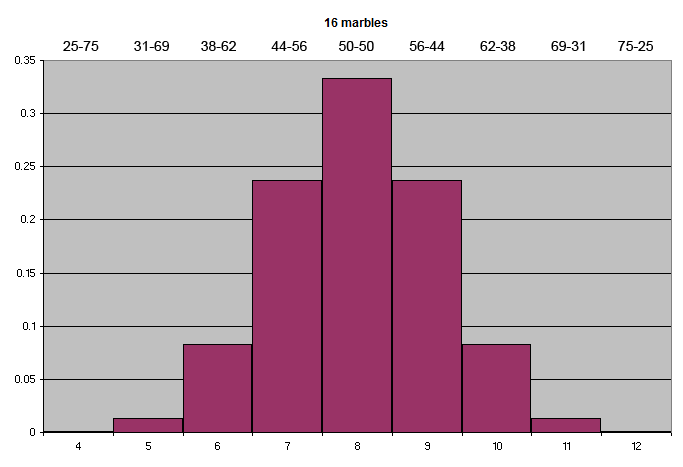
If one were really ambitious, one could vary the odds separately for each line.
Removing more marbles leads to more variation; but with a small number of marbles, the range of variation is sometimes not very satisfying, as it leads to high probabilities of having zero moving lines and so forth. One may start with more marbles; but at some point they become cumbersome and require a lot of handling. There is a much easier way to increase the possibilities . . . .
     
|
Using playing cards
Playing cards provide more opportunities for variation than beads or marbles, and are even easier to use. When using playing cards to determine I Ching lines, the approximate probabilities are similar to those of the yarrow stalk and coin methods. Black cards (spades, clubs) are yin lines; red (hearts, diamonds) are yang. Face cards (jack, queen, king) are moving lines.
| yarrow stalks | traditional coins | playing cards | ||||
| moving yin | 1/16 | 0.0625 | 1/8 | 0.125 | 6/52 | 0.115 |
| yang | 5/16 | 0.3125 | 3/8 | 0.375 | 20/52 | 0.385 |
| yin | 7/16 | 0.4375 | 3/8 | 0.375 | 20/52 | 0.385 |
| moving yang | 3/16 | 0.1875 | 1/8 | 0.125 | 6/52 | 0.115 |
One may vary the probabilities by simply cutting off a part of the deck, then using a smaller selected deck whose line probabilities are not known ahead of time. Consider a full deck of 52 cards. The probability of obtaining either a yin or yang line is always 26/52, or 50-50. But if you cut off 1/4 of the deck, leaving 39 cards, the distribution of probabilities is as follows:
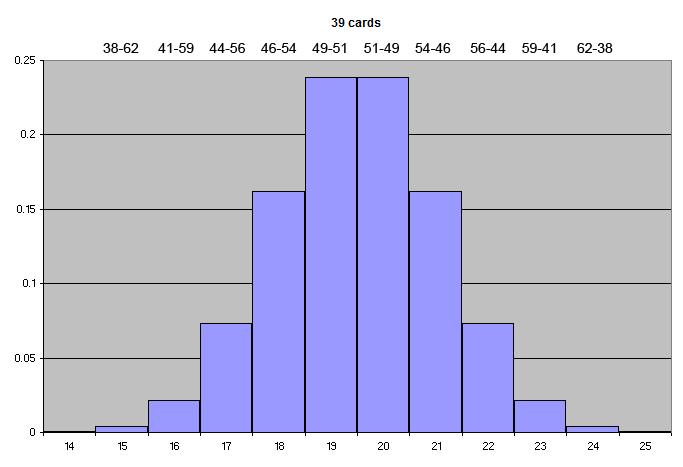
The graph illustrates that the odds of having 18 yang and 21 yin cards in a cut deck of 39 are 0.162, or 16.2%; the ratio of lines in that case is about 46-54.
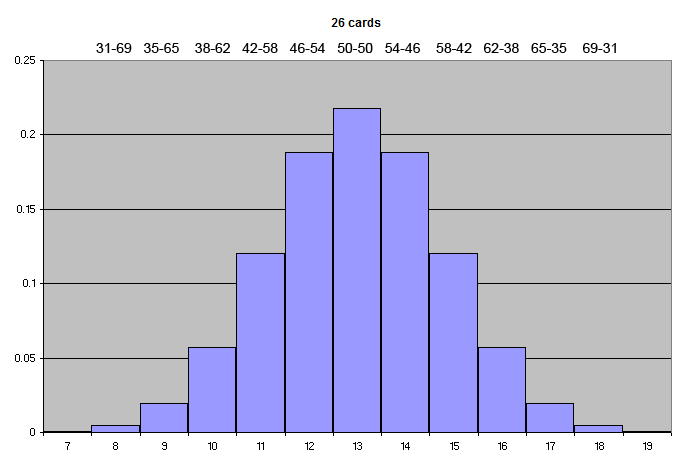
If you cut off 1/2 of the deck, leaving 26 cards, the range of distributions is wider, meaning that the results are less predictable:
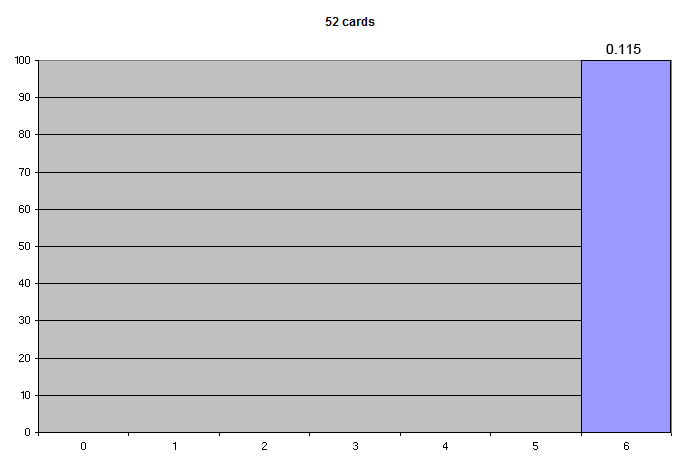
Using playing cards introduces even more variation into the ratio of moving lines. With a full deck of 52 cards, the probability of obtaining either a moving yin or yang line is always 6/52, or 0.115:
However, if you cut off 1/4 of the deck, leaving 39 cards, the distribution of probabilities of getting either moving line is now as follows:
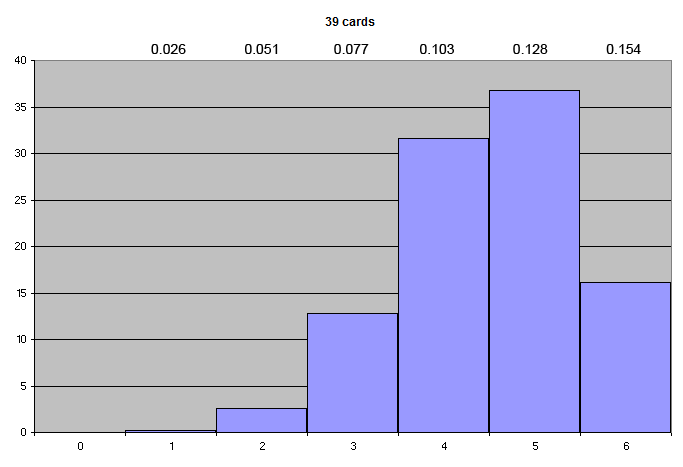
The odds of getting 5 moving lines in 39 cards, for example, is 0.368, or 36.8%; and when using that deck, the odds of getting a moving line are 5/39, or 0.128.
If you cut off 1/2 of the deck, the distribution is skewed even further:
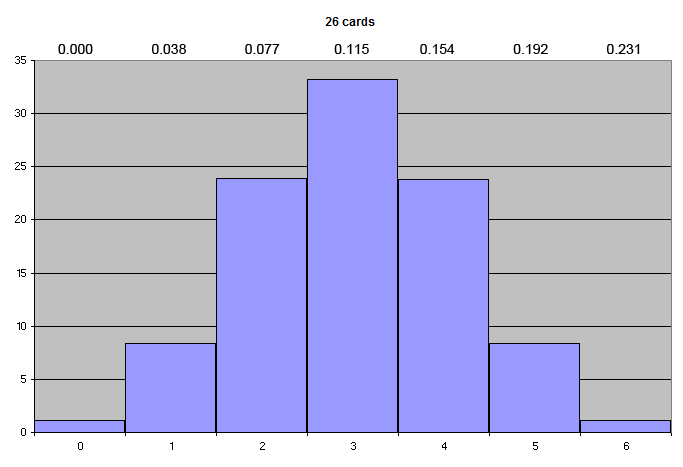
Using yarrow stalks, the probability of a moving yang line is 0.1875. Using a subset of 39 cards, the probability of either moving line ranges up to 0.154, and with 26 cards there is a small possibility going up to 0.231. So if you cut off 1/4 to 1/2 of the deck, you are skewing the odds along the lines of yarrow stalks, albeit in either direction for either yin or yang lines. There is a wider and more finely-variable range of probabilities when using cards than there is when using marbles. The choice that determines the odds is how many cards are removed from the deck, which will vary depending on the situation and one’s mindset.
Note that in the long run, the overall odds of getting either a yin or yang line are always 26/52, and those of getting either moving line are 6/52; cutting off part of the deck just makes the odds vary from hand to hand. The same principle applies when using beads or marbles. The point here is that you are letting the process determine its own odds for each situation. And the odds for moving lines vary independently for yin and yang; there are 6 moving lines of each color in a deck of cards.
If you remove two red and two black pip cards (non-face cards) from the deck at the beginning, the overall probabilities match those of the traditional coin method (6/48, or 1/8), and the odds of getting a moving line increase slightly.
Formal calculation of the probability ranges above is beyond me. (It is called “hypergeometric distribution”; there are online calculators.) I determined the probabilities by running simulations of a million “hands” and averaging the results. I am not going to tell you where I got the idea for this. You can try it yourself below. The population size is 52 for a deck of cards; successes in population would be 6 for the moving lines of one color. Sample size is the number of cards left after cutting; successes in sample is the number of moving lines in the cut deck. The output is the probability of getting that number of moving lines in the cut deck. (Or in math class terms, if you have a bag with 52 marbles, 6 white and 46 black, and you withdraw 26 marbles, what is the probability that 5 of those marbles will be white?) If your computer is slow, you may need to reduce the number of simulations (at the expense of accuracy).
For descriptions of the use of these methods, and JavaScript versions, see the dynamic playing cards page.
If you are using another type of deck, such as an I Ching oracle, or Tarot cards, you can let even-numbered cards count as 2 and odd-numbered cards count as 3, and deal three cards per line as if you were casting coins. In this case, cutting off a casual 1/2 of the deck, more or less depending on how you feel, gives a pleasant skew to the odds. I know you would love to see the graphs, but here are just some numbers to give you the general idea. When cutting a deck of 64 cards in half, the odds of getting 18 odd and 14 even-numbered cards are about 12%. In this case, the odds of getting a 6, 7, 8, or 9 as a line number are about 7%, 33%, 43%, and 17%, respectively, skewed a little toward moving yang. But interestingly, the relative odds of any yang vs. yin line are still 50-50. If you prefer to skew those odds in the same direction as those for moving lines, then use the mostly-yin or mostly-yang line method, where two evens and an odd are yin, and two odds and an even are yang. (Three of each still make the corresponding moving line.) The odds of any yang vs. yin line then become about 60-40.
(An easier way to use a Tarot deck is to let court cards and aces count as moving lines. Cups and coins are yin, swords and rods are yang. Even-numbered trump cards are yin, odd are yang. Then just cut off 1/4 to 1/2 of the deck as described above.)