The Chess960 Numbers Decoded
Convert to and from Chess960 numbers mathematically, without lookup tables
 

Go to the summary

  0 NNxxx Qxxxxx Bxxx Bxxx
  1 NNxxx Qxxxxx Bxxx xBxx
  2 NNxxx Qxxxxx Bxxx xxBx
  3 NNxxx Qxxxxx Bxxx xxxB
  4 NNxxx Qxxxxx xBxx Bxxx
  5 NNxxx Qxxxxx xBxx xBxx
  6 NNxxx Qxxxxx xBxx xxBx
  7 NNxxx Qxxxxx xBxx xxxB
  8 NNxxx Qxxxxx xxBx Bxxx
  9 NNxxx Qxxxxx xxBx xBxx
 10 NNxxx Qxxxxx xxBx xxBx
 11 NNxxx Qxxxxx xxBx xxxB
 12 NNxxx Qxxxxx xxxB Bxxx
 13 NNxxx Qxxxxx xxxB xBxx
 14 NNxxx Qxxxxx xxxB xxBx
 15 NNxxx Qxxxxx xxxB xxxB
 16 NNxxx xQxxxx Bxxx Bxxx
 17 NNxxx xQxxxx Bxxx xBxx
 18 NNxxx xQxxxx Bxxx xxBx
 19 NNxxx xQxxxx Bxxx xxxB
    96 total
 96 NxNxx Qxxxxx Bxxx Bxxx
    ...
192 NxxNx Qxxxxx Bxxx Bxxx
    ...
288 NxxxN Qxxxxx Bxxx Bxxx
    ...
384 xNNxx Qxxxxx Bxxx Bxxx
    ...
480 xNxNx Qxxxxx Bxxx Bxxx
    ...
576 xNxxN Qxxxxx Bxxx Bxxx
    ...
672 xxNNx Qxxxxx Bxxx Bxxx
    ...
768 xxNxN Qxxxxx Bxxx Bxxx
    ...
864 xxxNN Qxxxxx Bxxx Bxxx
    ...

The Chess960 numbering scheme devised by Reinhard Scharnagl begins with 10, 96-length blocks of each knight (N) position.  The N positions include only the knights, rooks, and king.  The rooks and king always fill the last three vacant squares in the order RKR, so they are indicated by x’s for simplicity and play no individual role in the determination of the Chess960 numbering.

Each N block is made of 6, 16-length blocks of each queen (Q) position; they consist of the pieces of the N position with the queen added, or the empty board squares after the bishops have been added.

Each Q block is made of 4, 4-length blocks of each dark-square bishop (B_b) position.

Each B_b block is made of 4, 1-length blocks of each light-square bishop (B_w) position.  The B positions consist of the four dark or light squares in the entire row of eight pieces.

NQBRNBKR

We will begin with this board position, and convert it to the Chess960 number mathematically.

First, we look at the N position.  (Note:  the location of each piece in a string of characters such as this is zero-indexed; it begins with zero on the left and increases to the right:  01234.)

NxNxx     N1=0, N2=2

Here is the list of all the N positions.  The number associated with the N position is multiplied by 96 as part of the position’s Chess960 number.  Is there a way to determine the N number of any position mathematically, without using the list?

0 NNxxx
1 NxNxx
2 NxxNx
3 NxxxN
4 xNNxx
5 xNxNx
6 xNxxN
7 xxNNx
8 xxNxN
9 xxxNN

The N₁ positions look like they belong to the series of triangular numbers:

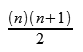
Looking at the series as if they were indexed from the right side, converting N₁ to the triangular number based on zero in the next-to-last position, and adding the index of N₂ based on zero in the last position, gives us a series that descends from 9 to 0.

9 = 6 Nxxxx + 3 xNxxx
8 = 6 Nxxxx + 2 xxNxx
7 = 6 Nxxxx + 1 xxxNx
6 = 6 Nxxxx + 0 xxxxN
5 = 3 xNxxx + 2 xxNxx
4 = 3 xNxxx + 1 xxxNx
3 = 3 xNxxx + 0 xxxxN
2 = 1 xxNxx + 1 xxxNx
1 = 1 xxNxx + 0 xxxxN
0 = 0 xxxNx + 0 xxxxN

So, subtracting the N₁ index from 3, and the N₂ index from 4, then subtracting the sum from 9, gives us an ascending series from 0 to 9:

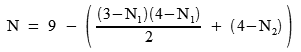
In our case, inserting the above N₁ and N₂ values reveals the N number:

N=9-(6+2)=1

The Q and B indices are much easier.  Inserting the Q from our original setup into the N position gives a Q index of 1:

xQxxxx    Q=1

Including the B’s, and separating out the dark and light squares, gives the B indices:

x B x x   Bb=1
xxBxxBxx
 x x B x  Bw=2

Putting it all together, and simplifying the N equation a little, this is how we find the Chess960 number directly from the N, Q, and B indices, without resorting to lookup tables:

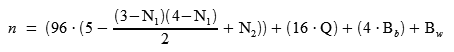
In our case, n = 118.

Starting with 118 as our Chess960 number, how do we mathematically determine the position that it represents, again without using lookup tables?

The B_w indices repeat in the sequence 012301230123 . . . .  So we start by finding the remainder when we divide n by 4, in terms of how many units are left over; this is called the modulo function, and in this case it tells us what the B_w index is.

Then we are going to divide n by 4, and throw away the remainder; this is called the floor function.  It lets us treat the B_b indices as if they repeat in the same 0123 sequence, and we can find the B_b index by the same modulo function.

Bw = n mod 4 = 2      x x B x
n = floor(n/4) = 29

Bb = n mod 4 = 1     x B x x
n = floor(n/4) = 7

Since the B_b indices also repeat in blocks of 4, we again divide n by 4 and throw away the remainder.  Now the Q indices repeat in blocks of 6:  012345012345012345 . . . , and n modulo 6 gives us the Q index.

Q = n mod 6 = 1      xQxxxx
n = floor(n/6) = 1

Now when we divide n by 6 and throw away the remainder, we are left with our N position number.  How do we determine the N₁ and N₂ indices, again without looking at the list?  Rearranging the N formula from above, we can find N₂ as a function of N₁.

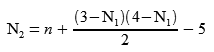
Each possible value of N₁ has a corresponding N₂ value.  How do we know which combination we want?  We know that N₁ is by definition less than N₂, and that the possible N₁ indices range from 0 to 3, and N₂ from 1 to 4.  The correct combination will uniquely satisfy the following conditions:

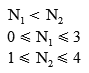
So all we have to do is try N₁ = 0, 1, 2, and 3 until we find the right one.  In our case,

N1=0, N2=2

So we know, without using the list, that the N position is

NxNxx

Now we can construct the position by starting with the B’s:

 x x B x  Bw=2
xxBxxBxx
x B x x   Bb=1

Adding Q = 1 to the empty squares:

xQBxxBxx

Then filling the empty squares with the N position gives:

NQBxNBxx

The remaining empty squares are filled with RKR:

NQBRNBKR

And we are back to our original board position.

Summary

Definitions:

NQBRNBKR
N  xN xx  N1, N2 indices (knights, rooks, and king)
xQ xx xx  Q index (queen added)
x B x x   Bb index (dark squares)
 x x B x  Bw index (light squares)

To convert a position to its Chess960 number:

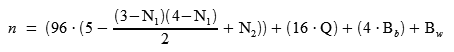
To determine a position from its Chess960 number:

Bw = n mod 4
n = floor(n/4)

Bb = n mod 4
n = floor(n/4)

Q = n mod 6
n = floor(n/6)

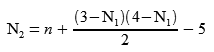
where

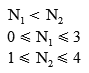
The entire list, with Shredder-FEN string, and mirror position:

p.s.  The above method of trying all possible N₁’s has something of a “brute force” quality to it.  Another way to find the correct combination is to begin with the following:

if n<4 then N₁=0
else if n<7 then N₁=1
else if n<9 then N₁=2
else N₁=3

and then use the equation to determine N₂.  But this method has a “lookup table” quality to it, and seems less “mathematical.”