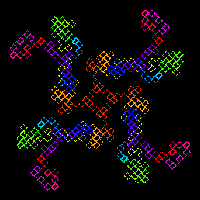What makes an image a fractal?
A defining feature of fractals is complex self-similarity at different scales.
For the Martin attractor, this is evident as one watches what happens while it grows as points
are added. It starts out as a small square or diamond, then puts out four “tentacles,” fills in to become a square or diamond again, then puts out four more tentacles to repeat the process. (Like an alien life form taking over a planet.) And significantly, you can’t tell by looking at it how large it has grown; the overall structure is similar at all scales.
Nothing to do? Watch the animation as the fractal grows from 10,000 to 2,000,000 points. It is continually rescaled and looks like it is receding, with the red ends of the tentacles coming toward you; by the end, what is left of the original image may only be a few pixels wide. If you have a slow computer, it may drag at high numbers. The parameters change every time it restarts.
Take it up to 10,000,000 | back to 2,000,000.
|
|

|
The points are colored with an RGB-CMY rainbow color palette in the order in which they are generated:
red, yellow, green, cyan, blue, magenta, and back to red.
The images thus tend to be red and yellow on the inside, and
magenta and red on the outside. But there are exceptions; as the growing ends waver back and forth, they sometimes “implode.”
You can see other evidence of self-similarity in the image to the right. Big blobs alternate with little blobs, and the center has a fractal-within-a-fractal appearance.
Another characteristic of fractals is sensitivity to initial conditions. You can see this for yourself at the
Fractal I Ching
page; tiny changes to the initial parameters produce totally different results, in a chaotic and nonlinear fashion.
The algorithm for the Martin attractor is an iteration of the following:
x1 = y0 - sin((b * x0) - c)
y1 = a - x0
I added the b and c parameters. The latter just adds another source of variability. Increasing b above 3 makes the results more interesting; the original Martin attractor has a tessellated appearance:
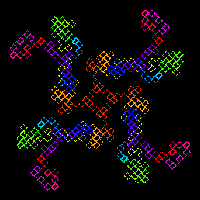
|
The Zaslavsky web map
is similar to the Martin attractor, but can be drawn with degrees of symmetry other than four. It is an iteration of the following:
x1 = (x0 + K sin(y0)) cos(α) + y0 sin(α)
y1 = −(x0 + K sin(y0)) sin(α) + y0 cos(α)
where α = 2π/q and q is an integer greater than 3. q determines the degree of symmetry in the figure and is easily chosen by the user. K should be greater than about 4 to keep the image from appearing tessellated.